

数学は、それ自身に内在する現象を探究する理論として、また、数学以外の諸分野の基礎付けを与える基礎科学として、あるいは、応用のための高度なツールとして発展してきました。
特に、現代は情報科学の著しい発展の最中にあり、これを数学的に正しく活用し、更に発展させていくことが重要です。
また、現代社会において高度な数学の活用・発展の期待も高いものとなっています。
数学・数理情報コースは、数学および情報科学の活用・発展の一翼を担うことで社会に貢献できる人材の育成を目的として、数学の広範な理論体系の基礎および情報科学の基本的知識・技能を教育するとともに、専門分野の枠を超えて協働できる能力を養う教育を行います。
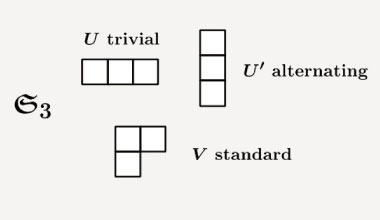
対称群の既約表現を記述するヤング図形
等式が織りなす精緻で深い理論
数の代わりに文字を用い、その記号的な操作・変換によって等式の仕組みを探求することを起源とする数学の一分野が代数学です。研究対象はいくつかの公理により定義された様々な代数系が主ですが、現代数学においては数学全般を学ぶ上で必要な共通言語を提供するという使命もあり、応用範囲が拡大し重要性が増してきています。

メビウスの帯
図形の包括的な研究
図形や空間が研究対象です。三角形や曲線・曲面のような素朴な意味での図形ばかりでなく、一見図形とは無関係そうな対象(代数方程式・微分方程式・行列…)も、図形や空間として扱える場合があるため、他の数学分野との交流が盛んです。また、物理や生物など自然科学分野と関わりが深く、より一層の発展が期待されています。
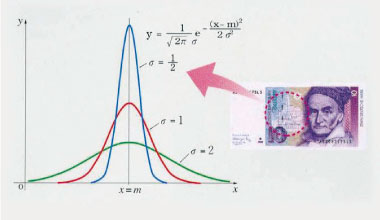
ドイツ紙幣にも描かれていたガウス分布
世の中の現象の解析に役立つ解析学
解析学は関数の性質などを調べる分野で、微分方程式論や確率論が含まれます。微分方程式は、世の中の現象を記述・解析するための道具です。熱の伝わり方を記述する熱方程式、天気予報に利用されるナビエ・ストークス方程式などがあります。一方、確率論は、偶然性の測定を目的とした分野です。統計や金融、保険などに利用されます。
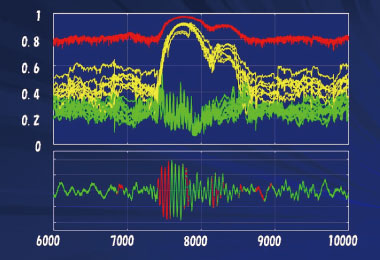
数理的に解析された地震波
情報化社会を支える先進分野
実社会で活用可能な数理的手法の開発を行っています。コンピュータは計算が得意ですが、自力でできるのは簡単な計算だけで、しかも、結果には誤差が付き物です。このため、誤差を小さくする処理は、私たち人間が考えます。画像や地震波などのデータ解析や、複数のコンピュータで役割分担して計算する場合にも、それを支えるのは数学です。
コース体系科目は、各専門分野の専門知識を体系的に学修するための科目群です。
コース課題科目では、セミナーや実験、実習を通して各専門分野の基盤スキルを身につけます。
| コース体系科目 | コース課題科目 |
|---|---|
| 集合と位相Ⅰ / 数学演習 / 代数学Ⅰ / 確率統計学Ⅰ / 集合と位相Ⅱ / 解析学Ⅰ / 代数学Ⅱ / 幾何学Ⅰ / 解析学Ⅱ / 数理情報処理Ⅰ / 代数学Ⅲ / 位相数学Ⅰ / 確率統計学Ⅱ / 幾何学Ⅱ / 解析学Ⅲ / 現象の数理 / 数理情報処理Ⅱ / 代数学Ⅳ / 解析学Ⅳ / 位相数学Ⅱ / 確率過程論 / 数値解析学A / 数値解析学B / 数理最適化A / 数理最適化B / 代数学Ⅴ / 幾何学Ⅲ / 位相数学Ⅲ / 解析学Ⅴ / シミュレーション論A / シミュレーション論B / 機械学習A / 機械学習B | 数学・数理情報セミナーA / 数学・数理情報セミナーB |
| 理学部共通基礎科目 | 理学部共通課題科目 |
|---|---|
| 数学の基礎 / 数理情報の基礎 / 数学Ⅰ / 数学Ⅱ / 物理学Ⅰ / 物理学Ⅱ / 化学Ⅰ / 化学Ⅱ / 化学Ⅲ / 化学Ⅳ / 生物学Ⅰ / 生物学Ⅱ / 地学Ⅰ / 地学Ⅱ / 基礎物理学実験 / 基礎化学実験 / 基礎生物学実験 / 基礎地学実験 | 科学研究倫理 / 特別演習Ⅰ / 特別演習Ⅱ / 課題研究 / 特別研究Ⅰ / 特別研究Ⅱ |
素朴な疑問から、新たな知見が生まれる。
数を数える・形を測る・変化をとらえる、といった素朴な問題を端緒とする数学ですが、高度な科学を駆使する現代に至るまで、いつの時代も変わることなく、「疑問を持つこと」が数学の発展の原動力です。
小・中学生が抱く四則演算や図形、関数についての素朴な疑問から、高校・大学で学ぶ代数・幾何・解析の諸問題、科学技術を支える応用的問題、そして数学者を悩ませ続ける世紀の難問まで「疑問」の程度は様々ですが、そこに優劣はありません。数学についての「疑問」に少しでも興味を持ち、先人たちの「知」の蓄積を学び、そしてその「疑問」を解決したい人。
また、数学的センスを生かして学校や企業で活躍したい人。そんな皆さんを、私たち数学・数理情報コースは心から歓迎しています。
| 氏名 | 研究テーマ | 個人ページURL |
|---|---|---|
| 教授 | ||
| 尾國 新一 | 非可換幾何学と幾何学的群論 | |
| ディミトリB.シャクマトフ | 位相群および位相体の位相構造の研究 | http://www.math.sci.ehime-u.ac.jp/~dima/ |
| 庭崎 隆(教) | 有限群論 | |
| 原本 博史(デ) | 擬似乱数、モンテカルロ法 | |
| 平野 幹 | 整数論(保型形式,保型表現とL関数) | |
| 松浦 真也 | 時系列解析 | http://www.math.sci.ehime-u.ac.jp/ ~matsuura/index.html |
| 山内 貴光 | 位相空間論 | |
| 山﨑 義徳 | 解析的整数論 | |
| 准教授 | ||
| 大塚 寛 | 並列プロセスとその間の通信に対する代数的アプローチ | |
| 大西 基也 | 学習理論と力学系の接点および制御ロボティクスへの応用 | https://www.math.sci.ehime-u.ac.jp/~mohnishi/ |
| 柳 重則 | 非線形偏微分方程式の研究および圧縮性Navier-Stokes方程式への応用 | |
| 講師 | ||
| 寺本 有花 | 解析学(圧縮性Navier-Stokes方程式の数学解析) | |
| 藤田 博司 | 記述集合論 | http://www.math.sci.ehime-u.ac.jp/~fujita/index.html |
| 助教 | ||
| 佐藤 拓也 | 非線形Schrödinger方程式の数学解析 | |
| 中島 啓貴 | 測度距離空間の幾何学 | https://hiroki-nakajima.github.io/ |
(デ)・・・データサイエンスセンター専任教員
(教)・・・教育・学生支援機構共通教育センター専任教員